(논문 요약) ARITHMETIC WITHOUT ALGORITHMS: LANGUAGE MODELS SOLVE MATH WITH A BAG OF HEURISTICS (paper)

핵심 내용

• LLM 은 어떻게 연산 문제를 푸는가? (e.g. 123+442)
  • general 한 계산 알고리즘을 구현하는가?
  • 데이터를 단순히 암기하는가?
  • 논문에서의 제안하는 내용: 여러 heuristics 들을 활용함.

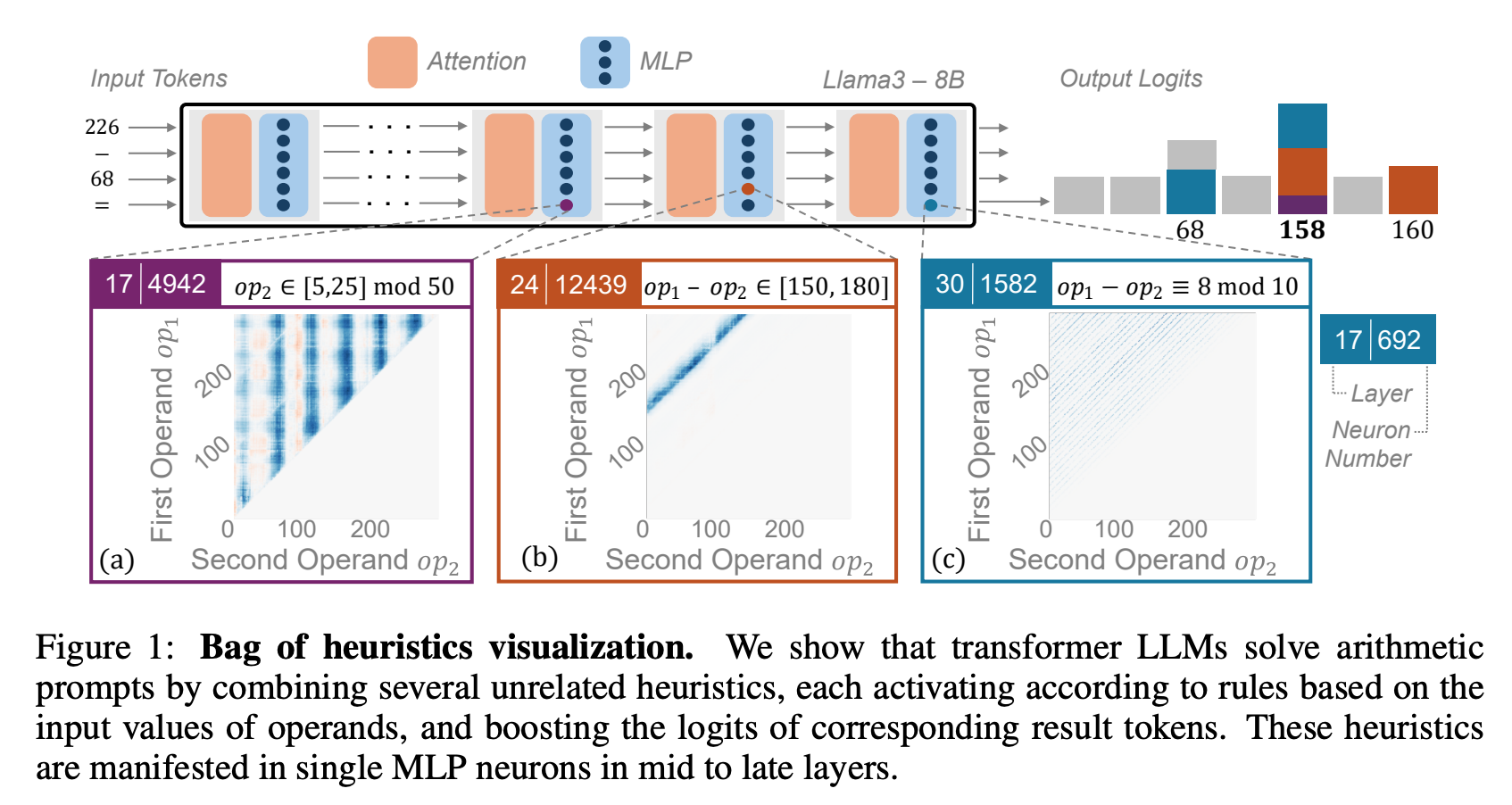
• Heuristic 의 예시
  

• MLP 에서 나타나는 pattern 관찰
  • “(op1)(operator)(op2)=” 을 prompt 로 입력
  • op1, op2, 연산 결과 가 [0, 1000] 으로, 각 숫자가 single token 인 경우 분석
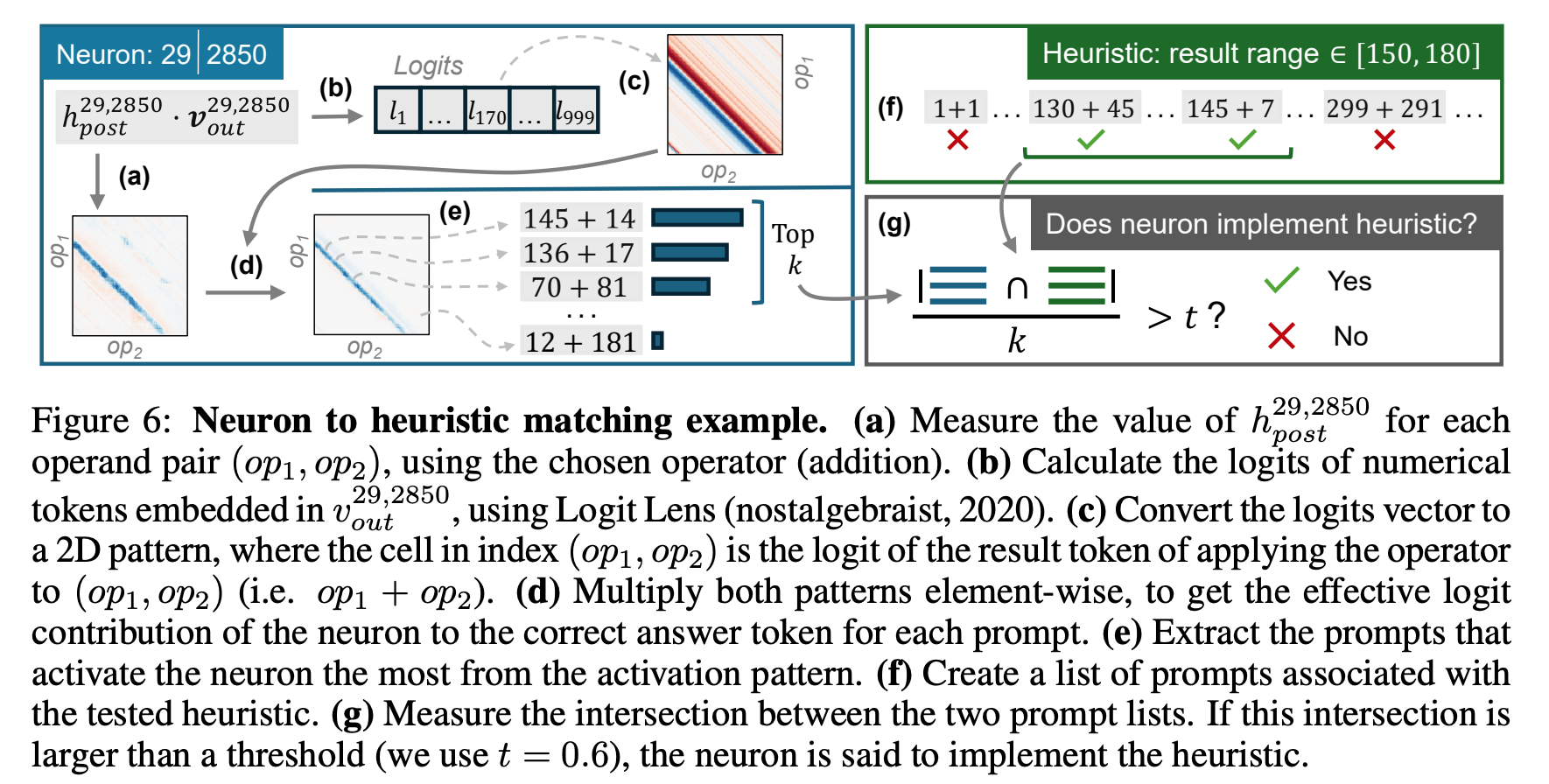
• 임의의 Heuristic 과 연관된 neuron 찾기
  • 특정 layer, neuron index 를 고정
  • (op1, op2) pairs 의 activation 값 계산 ($h_{post}^{l,i}$)
  • $v_{out}^{l,i}$ (weight 의 $i$ 번째 row) 를 Logit Lens 로 logit 계산 후, 정답에 해당하는 값들을 (op1, op2) pairs 로 추출
  • 위 2개 matrix 를 dot product
  • Top $k$ 에서 $k$: heuristic 을 만족하는 operands 쌍 개수

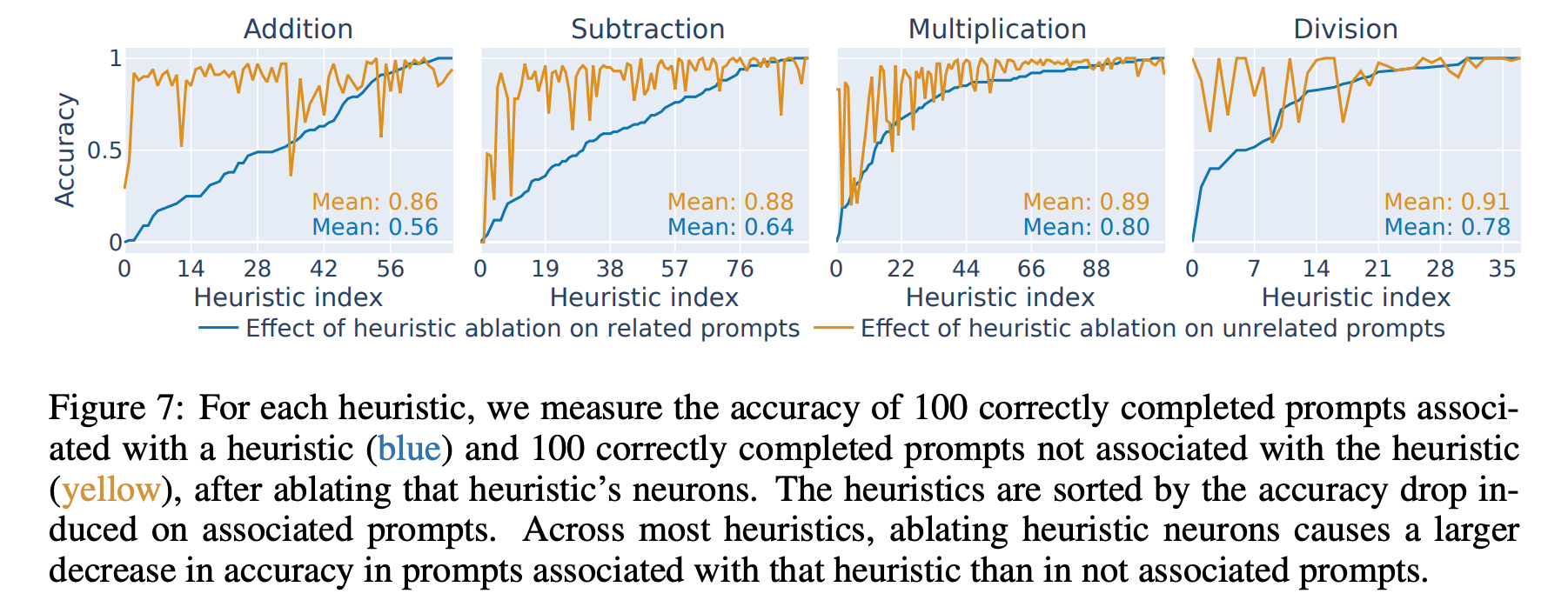
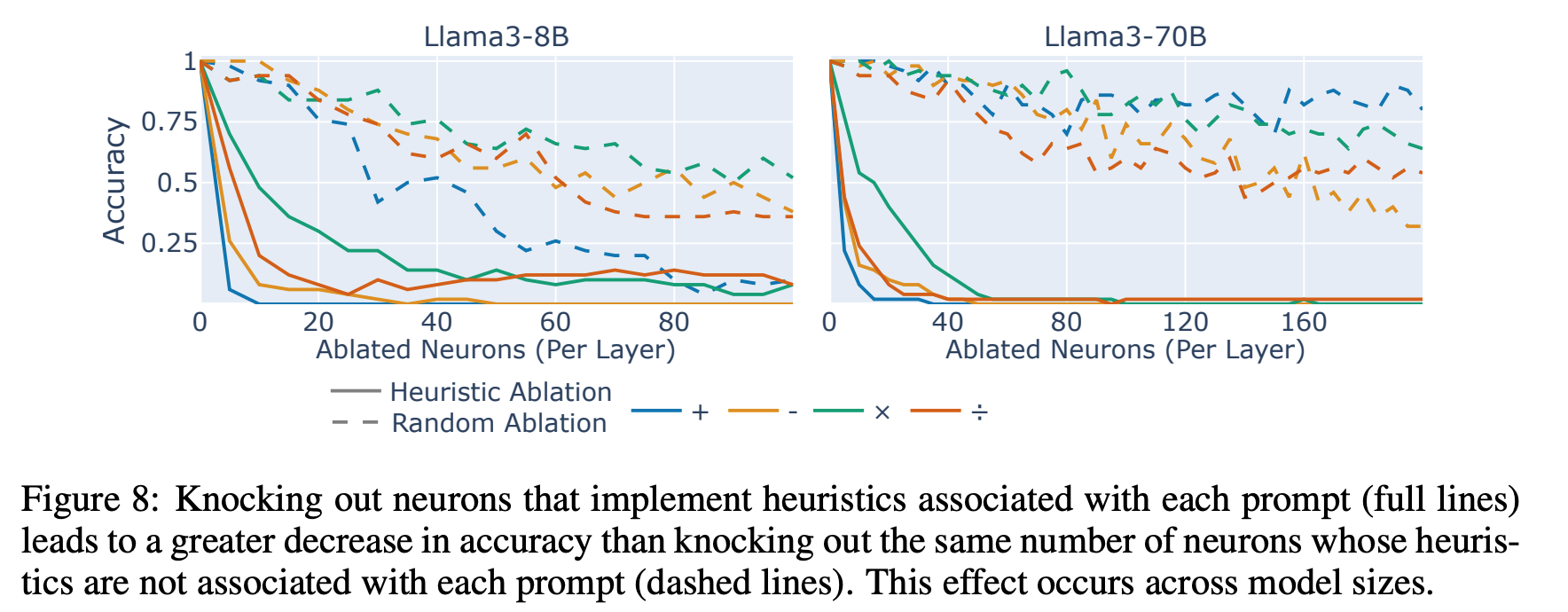
• 특정 heuristic 으로 classify 된 neuron 들의 activation 을 0 으로 두면 해당 heuristic 을 만족하는 문제를 잘 못맞춤.

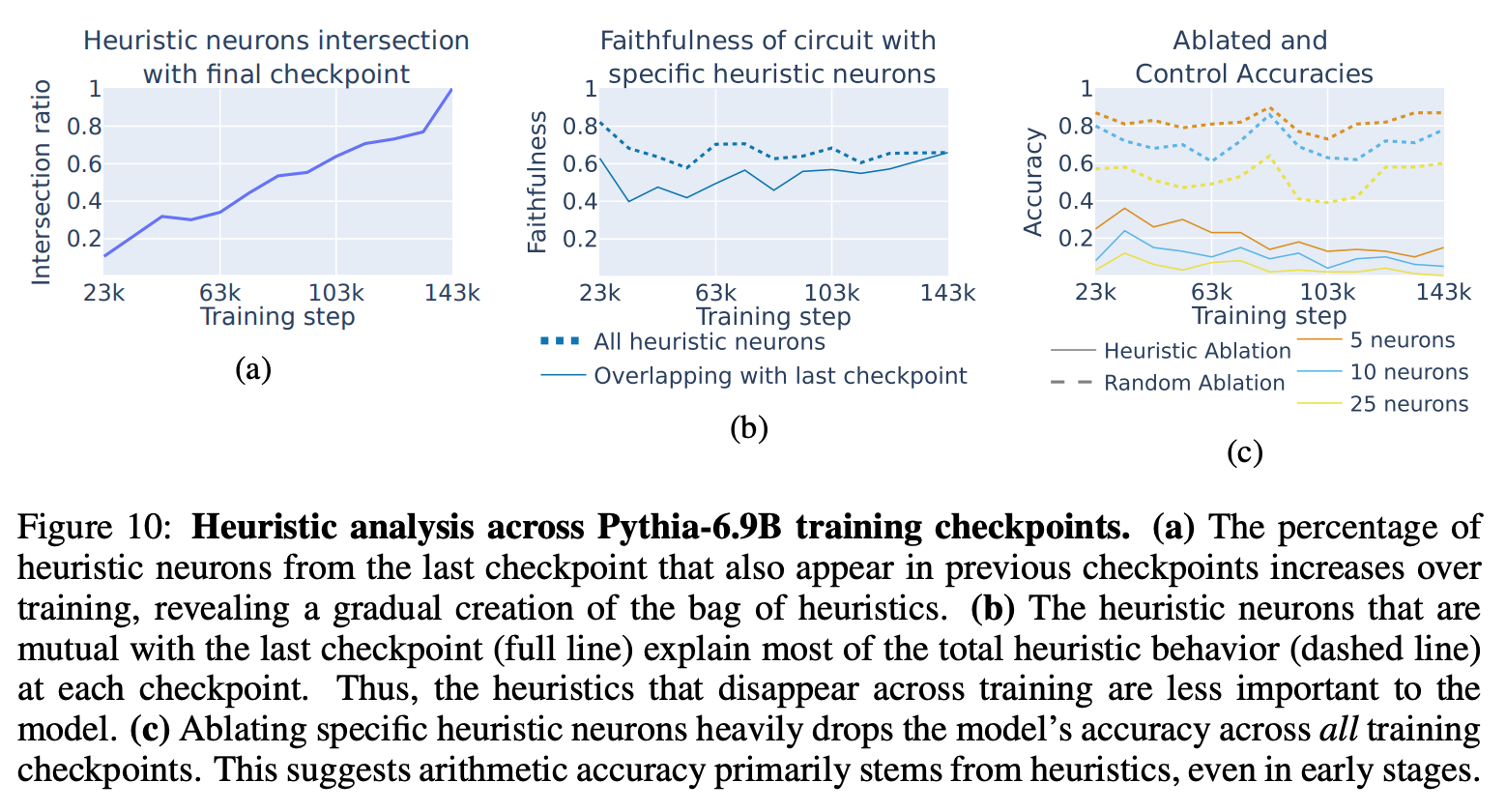
• 주어진 연산 문제에서 intersection score 가 가장 높은 neuron 들의 activation 을 0 으로 두면 성능이 급격히 떨어짐.
  

• 학습 과정 관찰
  • 최종 학습에서 얻어진 heuristics neurons 를 bag of heuristics 라고 하면,
  • (a) bag of heuristics 들은 선형적으로 증가함.
  • (b) bag of heuristics 은 학습 초기부터 중요한 역할을 함.
  • (c) heuristic neurons 들은 어떤 시점에도 중요한 역할을 함.