지표
- $r_n=\frac{p_n}{ma_n^w}$
- $p_n$: closing price at $n$th date
- $ma_n^w= \frac{1}{w} \sum_{i=0}^{w-1} p_{n - i}$: moving average with window size $w$
해석
- $r_n = r_{n+1} \leftrightarrow \frac{p_n}{ma_n^w}=\frac{p_{n+1}}{ma_{n+1}^w}=\frac{p_n+\Delta p_n}{ma_n^w+\Delta ma_{n+1}^w} \leftrightarrow \frac{p_n}{ma_n^w}=\frac{\Delta p_{n+1}}{\Delta ma_{n+1}^w}$
- $r_n < r_{n+1}$
- moving average 가 증가하는 경우: 가격이 더 증가.
- moving average 가 감소하는 경우: 가격이 덜 감소.
- $r_n > r_{n+1}$
- moving average 가 증가하는 경우: 가격이 덜 증가.
- moving average 가 감소하는 경우: 가격이 더 감소.
- Special cases
- $p_n=an+b$ 인 경우 $r\rightarrow 1$
- $p_n=ka^n$ 인 경우 $r=a$
- $p_n\rightarrow 0$ 인 경우 $r_n\rightarrow 0$
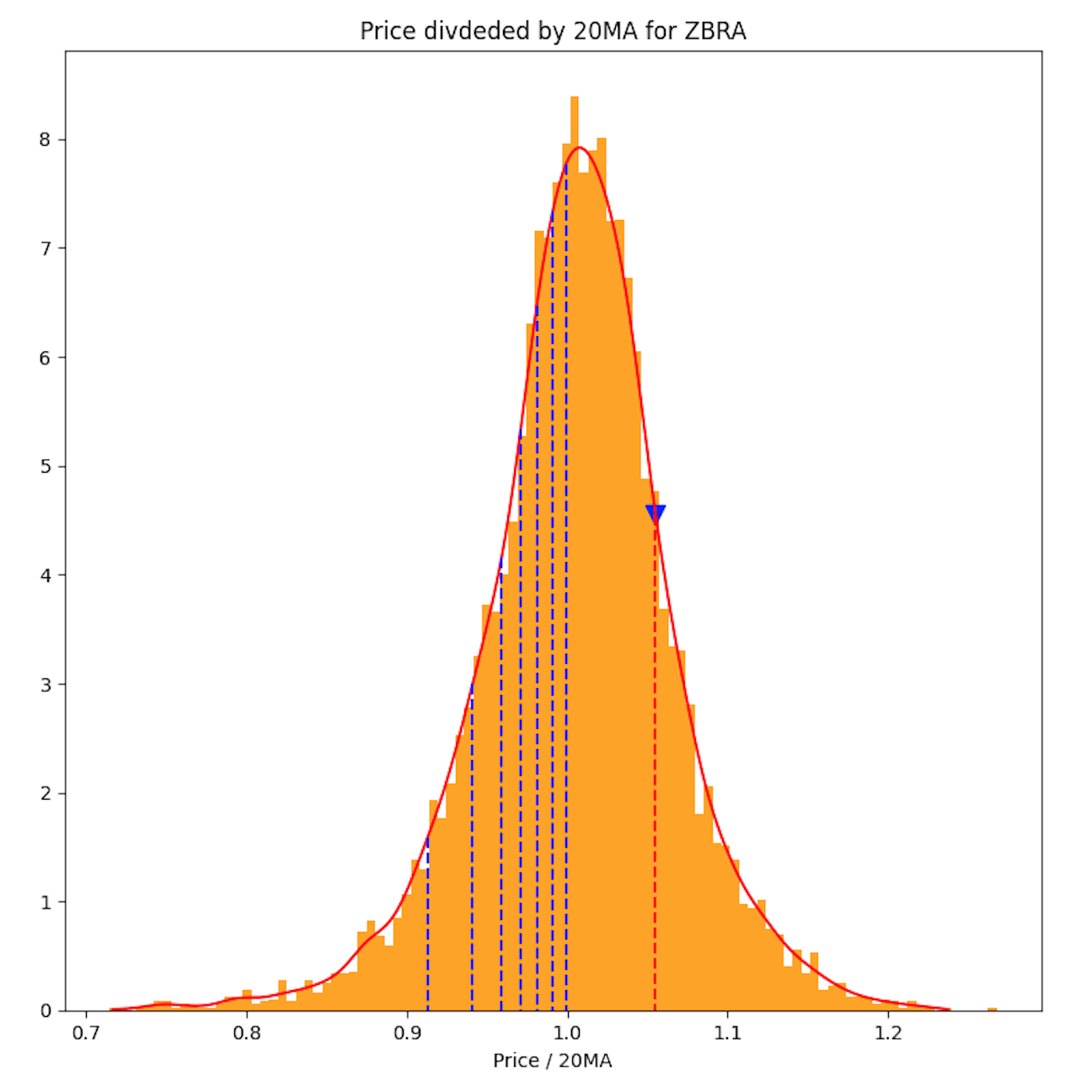
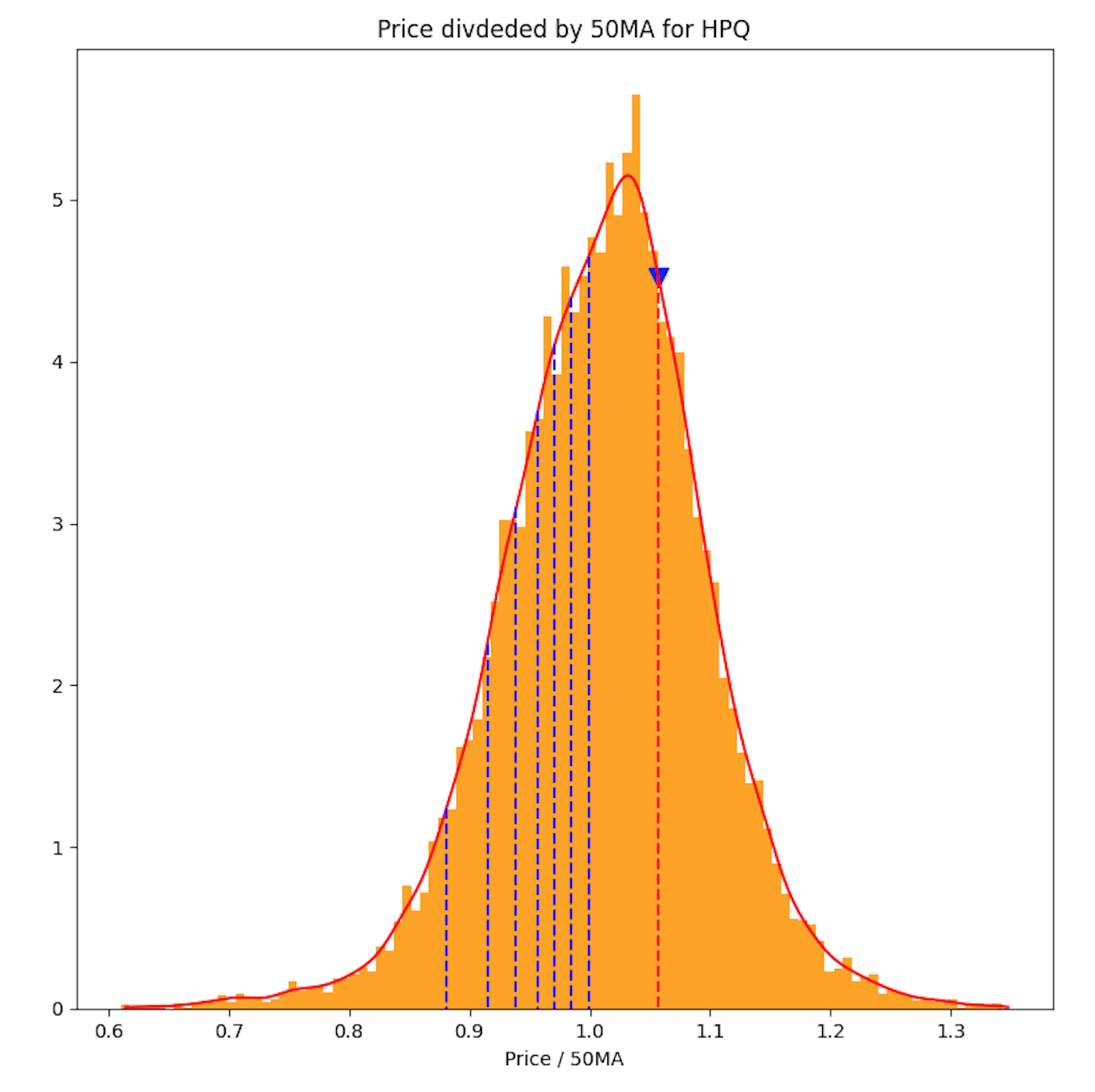
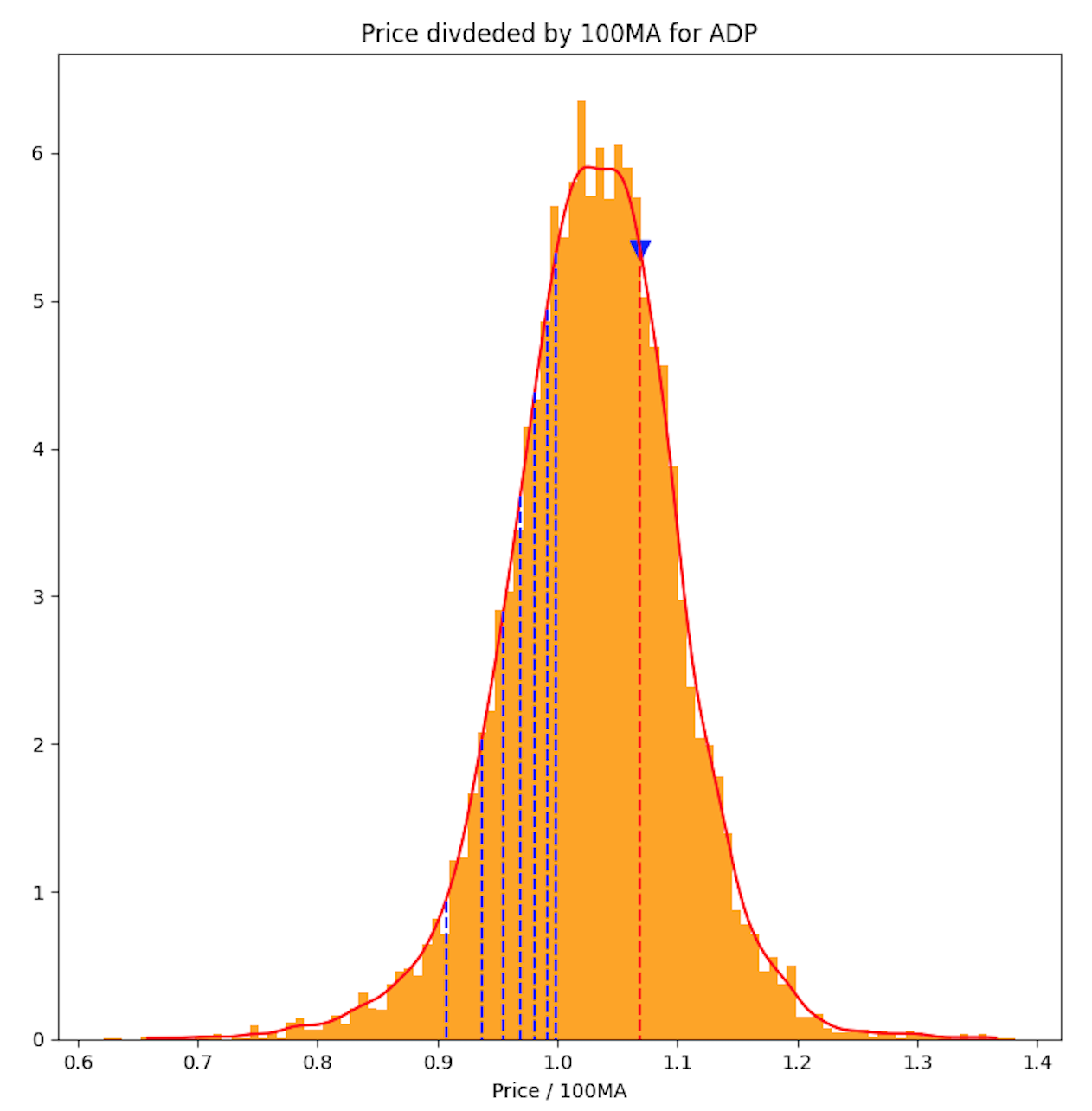
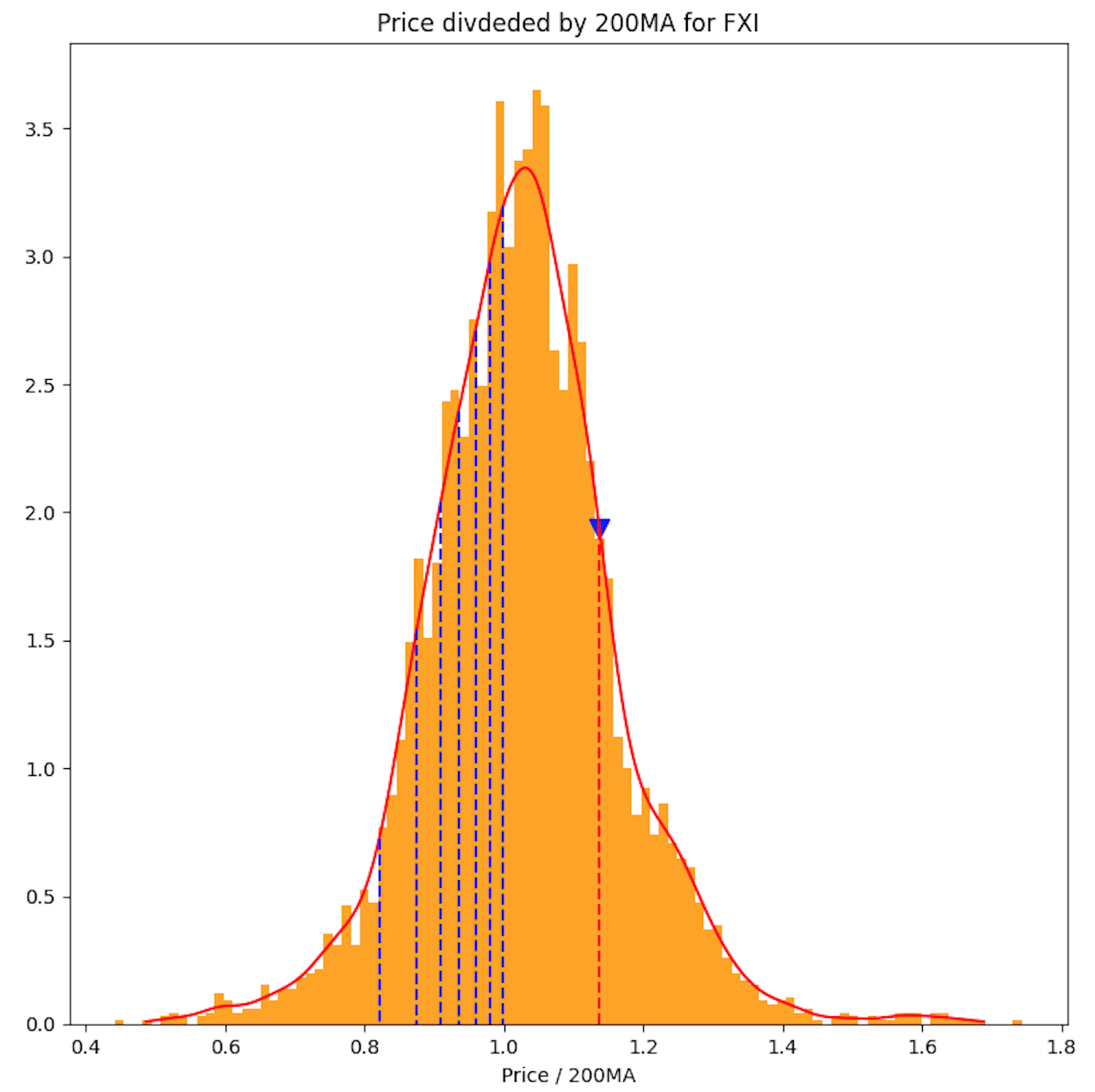
실제 주식에 대한 분포
- s&p 500 주식 및 주요 ETF (s&p500, nasdaq, semiconductor)
- 극단으로 갈수록 출현빈도가 낮아지는 경향성 (하한, 상한이 유한)
- 1 근처에 값이 모여있는 경향성